On Spaces of Coverings
yuliy baryshnikov
UIUC, mathematics and ECE
Introduction
One popular problem in applied probability deals with the coverage problem: place randomly $n$ disks of radii $r$ in a domain $Y$ (say, spherical caps on a sphere); what is the probability that their union covers the whole domain $Y$?
A great deal is known about this problem which can be formulated as follows:
Let $\cov_Y(n,r)\subset X^n$ be the collection of the centers of the disks such that their union covers $Y$.
What is its measure (with respect to some probability measure $\mu^n$ on $X^n$)?
Here we are interested not in the measure of the space $\cov_Y(n,r)$, but in its topology.
In slightly higher generality, let \(X, Y\) be topological spaces, and $R\subset X\times Y$ be an open subset of their product, a relation.
For $n\in\Nat$, we will define the space of $R$-coverings of $Y$ a collection $\bx$ of $n$ distinguishable points in $X$, $\bx=\{x_1,\ldots,x_n\}\subset $ such that for any $y\in Y$, there exists $x_k, 1\leq k\leq n$ for which $(x_k,y)\in R$.
In other words, the union of the slices $R_{x_k}, k=1,\ldots, n$ covers all of $Y$.
In this note we will be primarily concerned with the situation where $X=Y$ is a compact metric space, and the relation is given by $R=\{(x,y): d(x,y)\leq r\}$ for some $r>0$.
Definition An \((n,r)\)-covering as a collection of \(n\) distinguishable points in \(X\) such that the union of metric \(r\)-balls centered at these points contains all of \(X\). \[ \cov_X(n,r):=\{(x_1,\ldots,x_n)\in X^n|\cup_k B(x_k,r)=X\}\subset X^n \]
Sometimes one refers to such finite collections as $r$-net, or finite $r$-approximation of $X$ in the Gromov-Hausdorff metric.
Covering Intervals
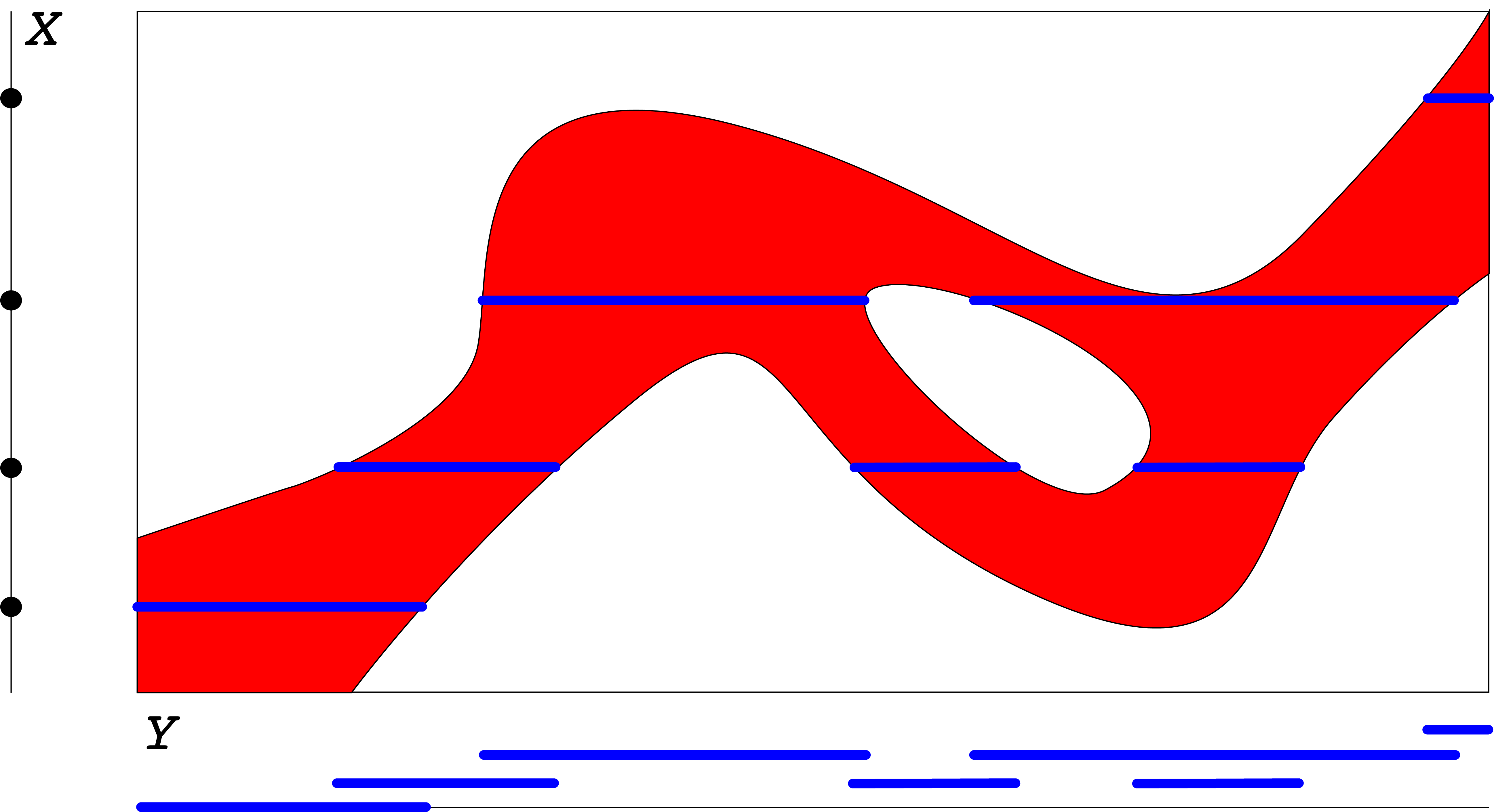
Let's take $X$ to be an interval (which we can assume to be $[0,1]$).
Let \(l\) be the smallest number of the open metric balls (i.e., the intervals of length \(2r\)) required to cover \(I\), - i.e. \[ l=\lfloor 1/2r \rfloor+1. \]
We define the slack as \(k=n-l\).
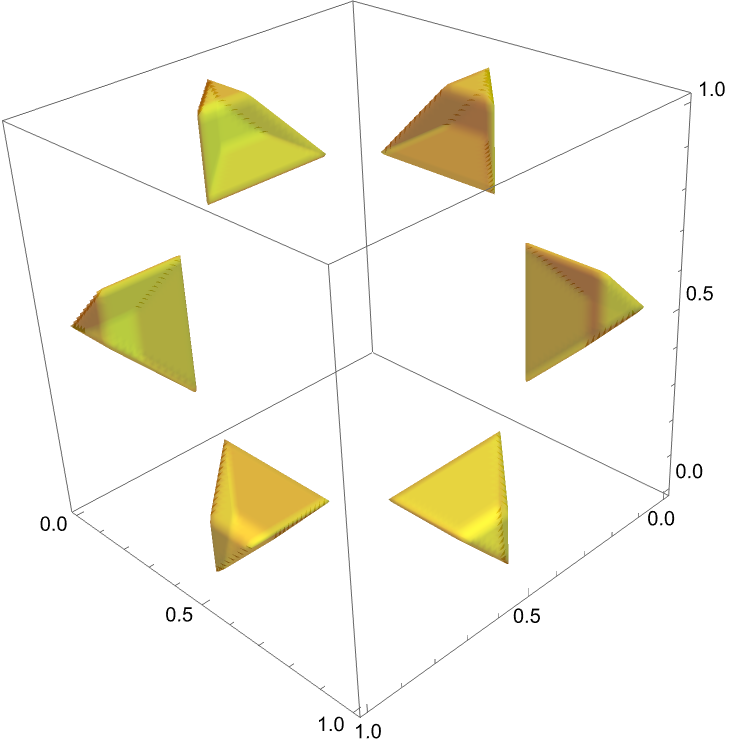
Two coverings of an interval of slack $5$.
Consider some examples for \(n=3\).
If the slack is zero (but the covering space is non-empty), the space of coverings consists of six components: the left-to-right order of the covering segments cannot be changed without breaking coverage. Each of the components is contractible.
Here, $r=.23$
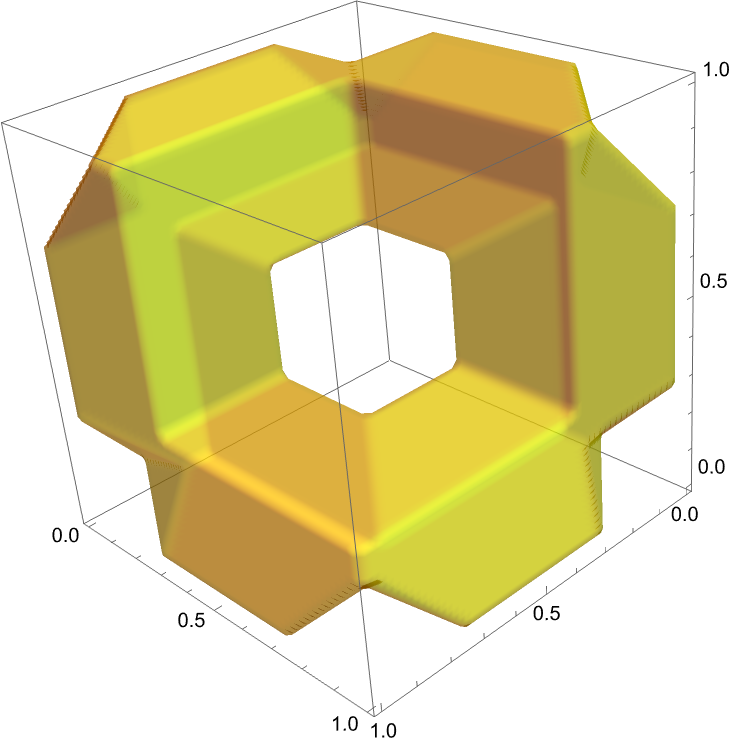
If the slack is one, the space is homeomorphic to the solid torus.
Here, $r=.36$
For general $r$, the topology of the space of coverings of an interval is given by the following
Theorem
The space of coverings $\cov_I(n,r)$ is homotopy equivalent to the $k$-skeleton of the permutahedron $P_n$, with $k=n-\lceil 1/2r\rceil$ being the slack: \[ \cov_I(n,r)\equiv \skel_k(P_n). \]
Here \(P_n\) is the order \(n\) permutahedron

On Permutahedra
Permutahedron is a convex polytope defined as the convex hull of the permutation orbit of a generic point $(a_1,\ldots, a_n)$, \[P_n=\mathtt{conv}\{(a_{\sigma_1},\ldots,a_{\sigma_n}),\sigma\in S_n\},\]
while \(\skel_k\) stands for \(k\)-skeleton, the union of all faces of the polyhedron of the dimensions \(k\) or less.

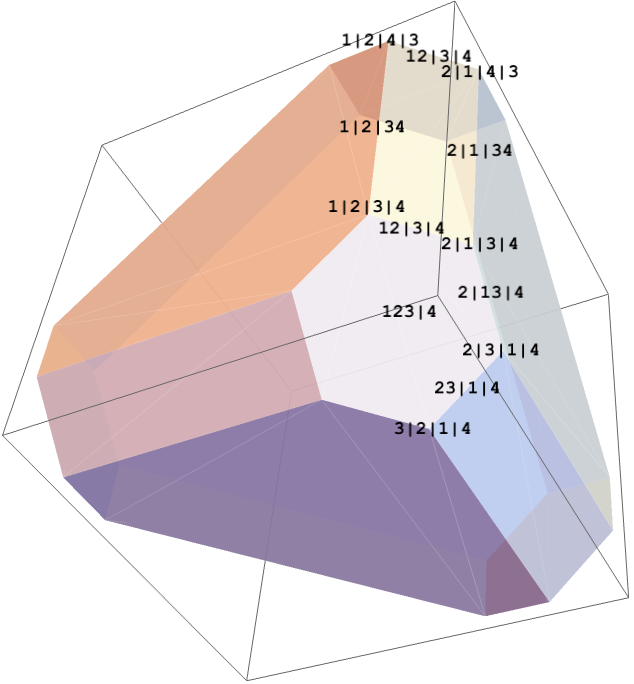
The vertices of $P_n$ correspond to the linear orderings on the set $\nset=\{1,2,\ldots,n\}$. The edges between these vertices correspond to transpositions of the neighboring elements in the linear order.
Each face of the permutahedron corresponds to a composition, i.e., a partition of \(\nset\) into an ordered sequence of disjoint blocks, considered as sets (unordered within each block). The compositions are naturally ordered (by the order-preserving refinements).
Each permutation can be considered as a composition into the blocks of size one. For a collection of linear orders, the (unique) minimal composition which can be refined to each of these orders corresponds to the minimal face of the permutahedron containing all the vertices corresponding to the permutations.
Conversely, for any composition the set of permutations obtained from it by various refinements into the linear order of singletons, forms the set of the faces on the boundary of the face corresponding to that composition.
In other words, we have
Proposition
The partially ordered set of the compositions of \(\nset\) is isomorphic to the lattice of the facets of the permutahedron \(P_n\). The dimension of the facet corresponding to the composition with $k$ blocks is $n-k$.
The $k$-skeleton of the permutahedron \(P_n\) is homotopy equivalent to the nerve of the sublattice of the compositions with at least $(n-k)$ blocks.
Topology of Permutahedra
Proposition
The \(k\)-skeleton of \(P_n\) is homotopy equivalent to a wedge of
\(k\)-spheres.
To find the homotopy type of the space of coverings of an interval it is enough to compute its Euler characteristics, \(\chi(\skel_k(P_n))\).
The exponential generating function for Euler characteristics of the skeleta of codimention \(k\) in \(P_n\) is \[ \sum_n \chi(\skel_k(P_n))\frac{z^n}{n!}= e^z-1-\sum_{l=0}^k(1-e^{-z})^{l+1}. \]
Examples
Codimension 1 \[ e^z-1-(1-e^{-z})=\sum_{n\geq 2} (1+(-1)^{n-2})\frac{z^n}{n!}: \] as expected, we recover the exponential generating function of Euler characteristics of $(n-2)$-dimensional spheres.
Codimension 2 \[ e^z-1-(1-e^{-z})-(1-e^{-z})^2=\sum_{n\geq 3}(1+(-1)^{n-3}(3-2^n))\frac{z^n}{n!}. \] In other words, the \((n-3)\)-skeleton of \(P_n\) is homotopy equivalent to a wedge of \(2^n-3\) spheres \(\sphere^{n-3}\), for \(n\geq 3\).
Forts and Details
There is a different way to look at the covering spaces \(\cov_I(n, r)\), in some sense dual to the permutahedron model.
Assume that $\forts$ is a finite set (the points of which are referred to as forts).
Definitions
- We call a surjective map from a subset of \(\nset\) to the set of forts \(\forts\) a detail (assigning guard to forts, so that all forts are covered).
- Details are partially ordered by adding guards: We say that a detail $\dl_1$ is dominated by $\dl_2$ (notation: \(\dl_1\prec \dl_2\)) if \(\dom(\dl_1)\subset\dom(\dl_2)\), and the restrictions of \(\dl_1, \dl_2\) to the domain of \(\dl_1\) coincide.
- Two details $\dl_1, \dl_2$ are compatible if their restrictions to the intersection of their domains coincide; in this case their {\em join} is defined as the detail whose domain is the union $\dom(\dl_1)\cup \dom(\dl_2)$ of their domains, and which is equal to $\dl_j$ on $\dom(\dl_j)$.
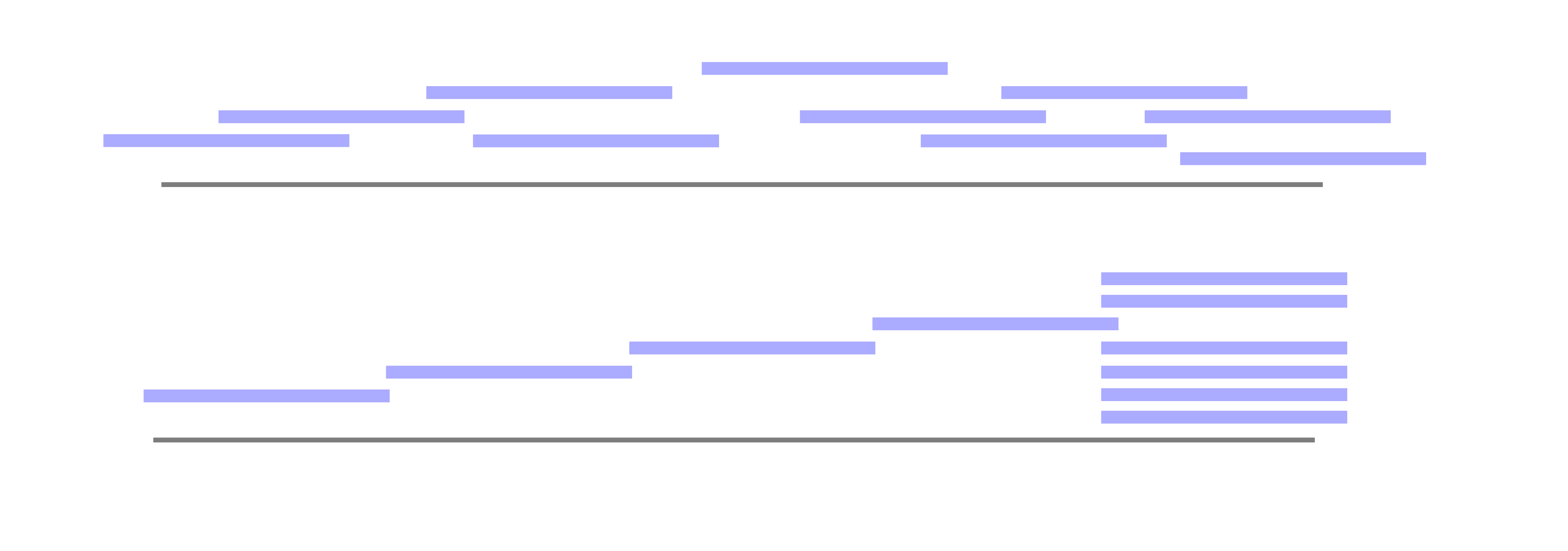
For fixed $\nset, \forts$, one can associate to the partial order on the details defined above its nerve (the simplicial complex whose simplices are chains in the poset) which we will denote as $\Delta(\nset,\forts)$.
Example For $|\forts|=2, n=3$, the partial order is shown on Figure, and its nerve has the homotopy type of a circle.
It turns out that the nerve $\Delta(\nset,\forts)$ of the posets of details is homotopy equivalent to an appropriate skeleton of a permutahedron:
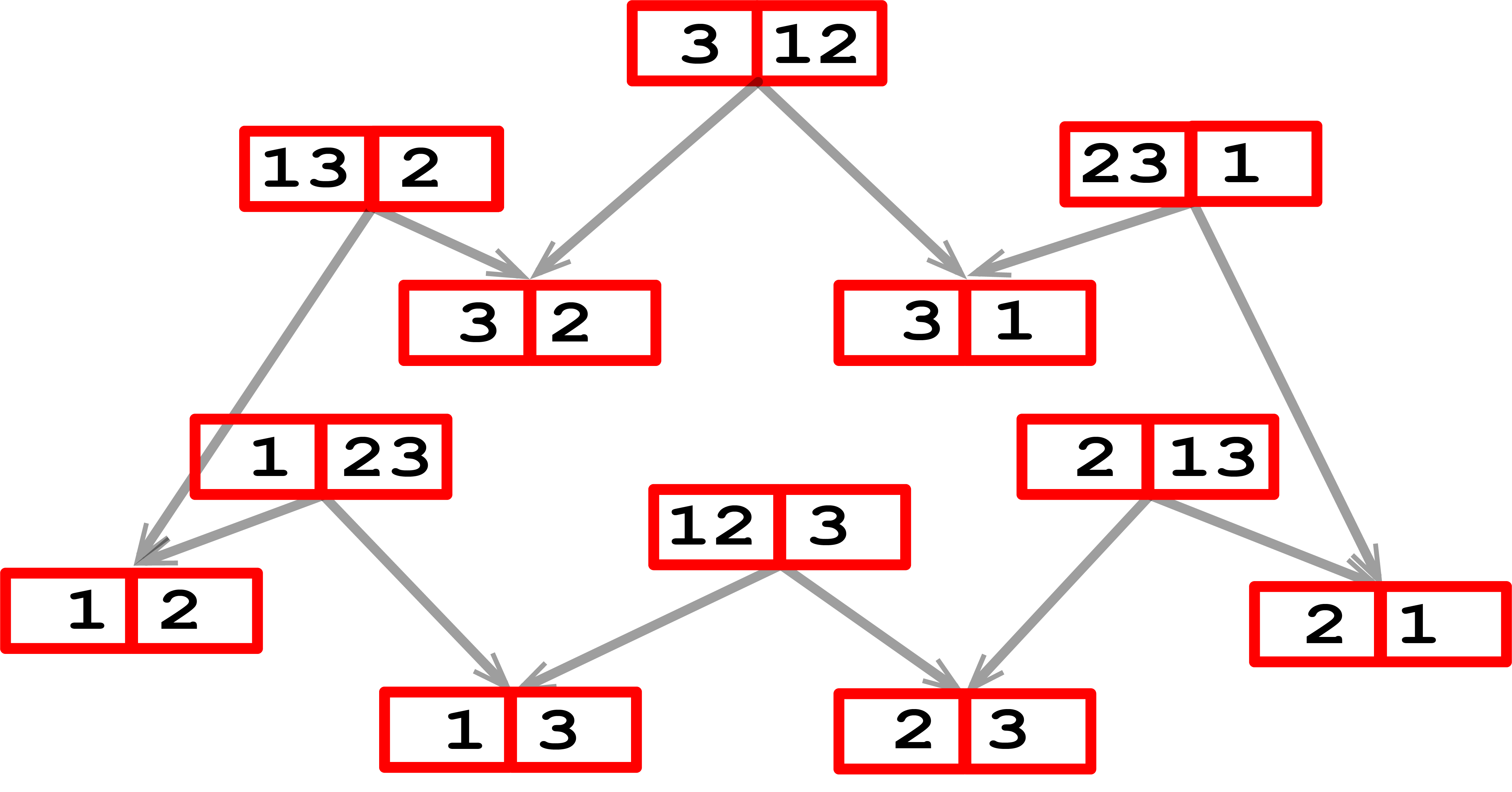
Proposition For any $n,\forts$, \(\Delta(n,\forts)\sim \skel_{n-|\forts|}(P_n). \)
Forts and Coverings of the Interval
We return now to the space of coverings of the interval, $\cov_I(n,r)$.
Define as forts $\forts$ the arithmetic progression with \(l\) terms, starting at \(0\) and ending at \(1\): \[ \forts =\{f_1=0, f_2=1/(l-1),\ldots,f_{l-1}=(l-2)/(l-1), f_l=1\}\subset I, \]
As the distances between the forts are \(1/(l-1)>2r\), no interval of length \(2r\) can contain more than one fort.
The subset of standard positions is an arithmetic progression of size $l$ such that $l$ intervals of length $2r$ with centers at the standard positions $\cent$ cover $I$: \[\cent=\{c_1\lt \cdots\lt c_l\}\subset I\]
For a detail $\dl$, call any configuration $\xx$ $\dl$-standard if $x_k$ is in the $\dl(k)$-th standard position for any $k\in\dom(\dl)$.
The collection of $\dl$-standard configurations is a closed contractible (indeed, homeomorphic to $I^{n-l}$) subset of $\cov_I(r,n)$.
Definition
For a detail $\dl$ we define the subset of $\dl$-admissible configurations in $\cov_I(n,r)$ as
\[
U_{\dl}:=\{\xx\in\cov_I(n,r):|f_{\dl(k)}-x_k|\lt r\},
\]
i.e., the collection of coverings such that the $k$-th interval contains
$\dl(k)$-th fort.
Any $\dl$-standard configuration is in $\dl$-admissible.
If a detail $\dl_1$ dominates the detail $\dl_2$, their admissible subsets satisfy $U_{\dl_2}\subset U_{\dl_1}$.
More generally, the lattice structure on the details maps contravariantly into the lattice of $\dl$-admissible sets:
Lemma The intersection of admissible sets over a family $D$ of details is the admissible set $U_{\dl^*}$, where $\dl^*$ is the join of details in $D$: \[ \bigcap_{\dl\in D} U_\dl=U_{\dl^*}, \dl^*=\bigvee_{\dl\in D} \dl. \]
Diagrams of Spaces
We are now in the situation known in the applied homotopy theory as an arrangement: a lattice of the subsets of a space is given such that their union is the whole space, and each of the embeddings in the lattice is a cofibration.
Recall now one of the standard results:
Proposition
If all subspaces in the poset of the subsets covering a space are contractible, then the ambient space is homotopy equivalent to the nerve of the poset.
Example For lattice of composition $I=(I_1|I_2|\ldots|I_l), l\leq k$ with $\nset=\amalg_j I_j$, the lattice of sets \[V_I:=\{\xx \ | \ x_m\lt x_{m'} \mbox{ if } m\in I_j, m'\in I_{j+1}\}\] is homotopy equivalent to $\skel_k(P_n)$.
The admissible sets are contractible:
Lemma
For every detail $\dl$, the set of $\dl$-central configurations is a deformation retract of $U_{\dl}$. In particular, every $U_\dl$ is contractible.
The proof is by sweeps:
This immediately produces a proof of
Proposition For any $n,\forts$, \[ \Delta(n,\forts)\sim \skel_{n-|\forts|}(P_n). \]
In fact, the same reasonings can be used in a general setting: assume that $X$ is a compact metric space.
Proposition
If $\forts\subset X$ is a finite subset of forts which are $2r$-separated, then
for any detail $\dl$ the subspace $U_\dl\subset \cov_X(r,n)$ of $\dl$-admissible configurations is well-defined, the space of $r$ coverings $\cov_X(r,n)$ is covered by the sets $U_\dl, \dl\in\dls$, and the lattice of details maps contravariantly to the lattice of the sets $U_\dl$.
In particular, if all $U_\dl$ are contractible, $\cov_X(r,n)$ is homotopy equivalent to the corresponding skeleta of the permutahedra.
A historical remark: the link of the admissible sets $U_\dl$ to the standard sets (where all the points $x_k, k\in\dom(\dl)$ are in the standard positions) was suggested by Hang Wan in his 2013 thesis. He studied specifically the unions of the sets with all standard positions occupied, and established that their homotopy types are independent of the set of standard positions.
Those spaces were rediscovered recently by D. Kozlov under the name of Stirling complexes.
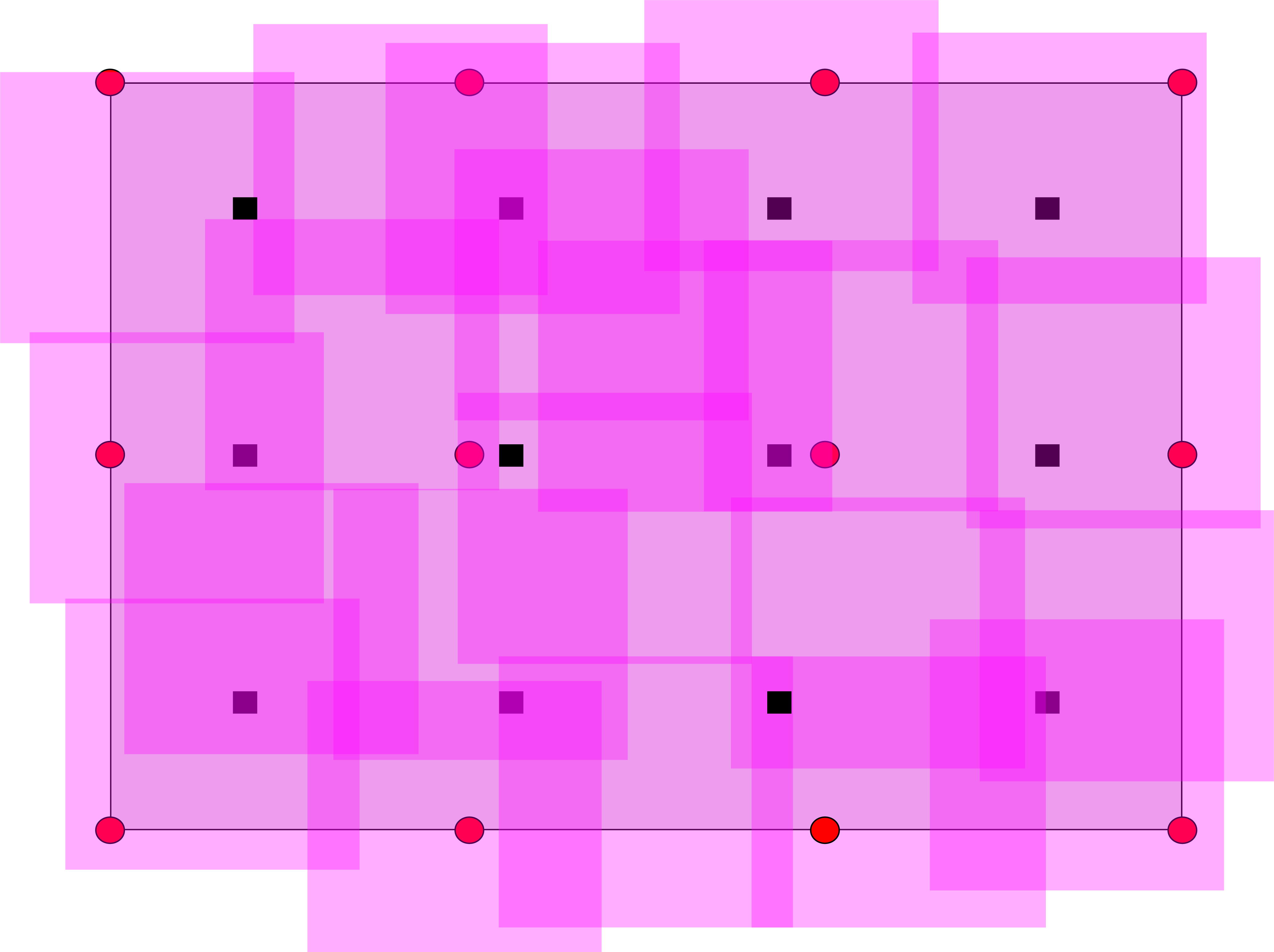
Covering Rectangles with $l_0$ Balls
We can generalize the theorem on the covering spaces of intervals to higher dimensions.
One situation where this is feasible is the problem of covering of a product of intervals by a collection of unit cubes.

Consider $X=\prod_{j=1}^d I_j$.
Let $l_j=\lfloor |I_j|/2r\rfloor+1$ is the minimal number of $2r$ 1D-balls needed to cover the interval $I_j$.
Then $l:=\prod l_j$ is the minimal number of $r$-balls in $l_0$ metric on $\Real^d$ needed to cover $X$. Define the slack as usual, $k=n-l$.
Theorem The space of $r$-coverings is homotopy equivalent to $k$-skeleton of $P_n$: \[ \cov_X(n,r)\sim \skel_k(P_n). \]
Theorem The space of $r$-coverings is homotopy equivalent to $k$-skeleton of $P_n$: \[ \cov_X(n,r)\sim \skel_k(P_n). \]
The proof is still by sweeps: one defines the forts, details and standard positions as in the univariate case. The key observation is that the sets $U_\dl, \dl\in \dls$ are still contractible.

Conclusion
What about other spaces of coverings? They seem to be much harder to study, not unlike the spaces of configuration of the hard disks in a bounded domain in $\Real^d, d\geq 2$.
Coverings through relations form a broad class of interesting examples, - wide open area.