\(\def\Real{\mathbb{R}}\def\tree{\mathcal{T}}\)
Consider a path metric space \(M\) and a continuous function \(f:M\to \Real\). For simplicity, all such pairs here will have sublevel sets of \(f\) compact (so that the function is bounded from below).
Then one can form the so-called merge tree (see, e.g. here, for motivation, and some history), a new topological space (let’s call it \(\tree(M,f)\)) which is defined as the factor of \(M\) by an equivalence relation. To define this equivalence relation, we say that \(x\in M\) tops \(y\in M\) if there is a path connecting \(x\) and \(y\) such that the pull back of \(f\) to the path attains its maximum at the \(x\) end, or equivalently, if \(y\) lies in the path-component of the set \(\{f\leq f(x)\}\). If \(x\) and \(y\) top each other, we say that they are equivalent: \(x \sim y\). The function \(f\) is constant on the equivalence classes, so we define the set \(\tree(M,f)\) of these classes, and give it the roughest topology in which this induced function (we still will call it \(f\)) is continuous.
Given two pairs \((M,f)\) and \((N,g)\) of spaces with continuous functions on them, one can form a new one: we denote by \(f\oplus g\) the function taking \((x,y)\in M\times N\) to \(f(x)+g(y)\).
For historical reasons, we will call this the Thom-Sebastiani addition.
Remarkably, one has the following
Proposition: The merge tree \(\tree(M\times N ,f\oplus g)\) depends only on the merge trees \(\tree_f:=\tree(M,f)\) and \(\tree_g=\tree(N,g)\).
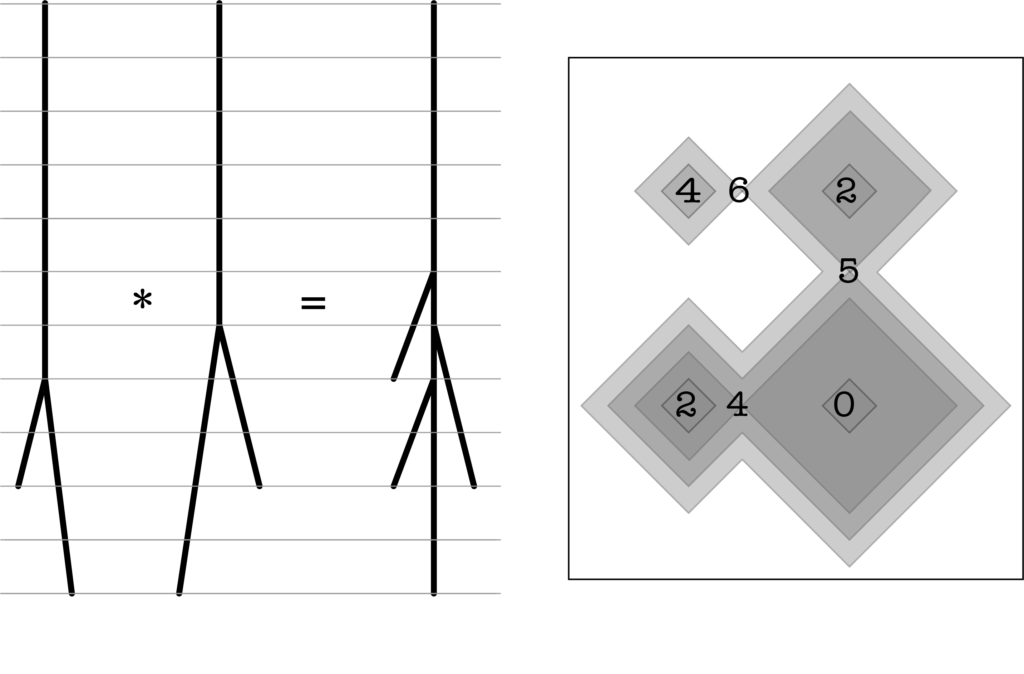
On the left, the \(\oplus\) of two merge trees \(\tree_1,\tree_2\) is shown. Each of the trees can be seen as the merge tree of its Dyck path: start at the root and visit all the vertices, left-to-right, breadth first; record the height, – that gives you a function on the time interval. Take the sum of these function on the product of the intervals, the result is the function on the right; its merge tree is, as expected, \(\tree_1\oplus\tree_2\).
We remark that the operation of taking the merge tree is idempotent: merge tree of a merge tree is itself.
Therefore, for a pair of merge trees, one can form their \(\oplus\)-sum. We will denote this merge tree simply as \(\tree_f\oplus\tree_g\).
Theorem: The operation \(\oplus\) turns merge trees into the monoid with unity (merge tree of the function \(x^2\) on \(\Real\)).
Note that the merge trees \(\tree_r\) corresponding to \((\Real,x^2 + r)\), i.e. trees \(\tree_r\) with a single leaf at the height \(r\), form an embedding of \(\Real\) into the merge trees monoid. Addition with such trees realizes the action of \(\Real\) on the merge trees, which shifts the height function by \(r\). We will denote this action as \[s_r\tree:=\tree+\tree_r.\]
There is a natural metric on the space of the merge trees. To work it out, we start by defining a morphism \[h:(M,f)\to(N,g)\] between pairs (space, function) as a continuous mapping \(h:M\to N\) such that \(f=h^*g\). One can immediately see that any such morphism induces a canonical morphism \[\tree(h):\tree_f\to\tree_g\] between the corresponding merge trees.
The monoid addition behaves well with respect to morphisms: a morphism \(h:(M,f)\to (M’,f’)\) induces naturally a morphism \[\tree(h)\oplus g:\tree_{f\oplus g}\to\tree_{f’\oplus g}\] for any merge tree \(\tree_g\).
For a merge tree \(\tree\) and \(r\geq 0\), there is a (unique) morphism \[\tree_r\to \tree\] that takes any point \(x\in\tree_r\) to the point \(y\in\tree\) at the same height, which tops it (recall that \(\tree\) and \(\tree_r\) coincide as topological spaces, but differ in their height functions by \(r\)). We will denote the resulting continuous mapping (not morphisms!) shifting the height by \(r\) as \(\sigma^\tree_r:\tree\to\tree\).
Remark. The range of \(\sigma^\tree_r\) is what is known as the \(h\)-trimming of the tree \(\tree\) (see Evans or Schertzer). The \(0\)-dim persistent diagram of the tree under trimming undertakes \(h\)-slide: all bars \((b,d)\) move to \((\min(b+h,d),d)\), while the adjacency relations are preserved.
Definition. We say that the distance between \(\tree, \tree’\) is at most \(\epsilon\) if there are morphisms
\[h:\tree_r\to\tree’, h’:\tree’_s\to\tree\] such that \[h’\circ h=\sigma^\tree_\epsilon, h\circ h’=\sigma^{\tree’}_\epsilon.\]
(Clearly, in this definition \(r+s=\epsilon\).)
A combination of these observations implies
Theorem Thom-Sebastiani addition is continuous: if the distance between trees \(\tree_f,\tree_{f’}\) and \(\tree_g,\tree_{g’}\) are less than \(\epsilon\), then the distance between \(\tree_{f\oplus g}\) and \(\tree_{f’\oplus g’}\) is less than \(2\epsilon\).
It is well known that 0-dimensional persistence diagrams of a function depends only on the merge tree. Remarkably, the persistence diagram of TS sum of two functions depend only on the persistence diagrams of either.
The applications of the TS addition on merge trees could perhaps come from compositionality ideas: the structure of the composition of two systems whose operational landscapes depend on the level of the available resources (energy), and which can trade those levels dynamically, but otherwise are independent, can be reduced to the addition of the corresponding merge trees.
Other applications include corner percolation (where one studies the structure of the level sets of functions \(f(x)-g(y)\) where \(f, g\) are (univariate) random functions representing the trajectories of random excursions of equal height), or merge trees of (tilted) Brownian sheets.
