The goal of this note is to define the biparametric persistence diagrams for smooth generic mappings \(h=(f,g):M\to\Real^2\) for smooth compact manifold (M). Existing approaches to multivariate persistence are mostly centered on the workaround of absence of reasonable algebraic theories for quiver representations for lattices of rank 2 or higher, or similar artificial obstacles.
Singularities of mappings into the plane
We will rely on the standard facts about generic smooth mappings into two-dimensional manifolds: for such mappings, the set of critical points is a smooth curve \(\Sigma\) in \(M\), which is immersed outside of a finite number of pleats: near generic point of \(\Sigma\), there are local coordinates on \(M\) in which the mapping is locally given by
\[
y_1=x_1, y_2=q(x_2,\ldots,x_m)
\]
(folds), and near isolated points of the curve of critical points, in some coordinates the mapping is given by
\[
y_1=x_1, y_2=x_2^3+x_1x_2+q(x_3,\ldots,x_m),
\]
(pleats). Here \(q\) is a quadratic form of the remaining variables (absent in the pleat case, if \(m=2\).
The image of the critical curve \(\Sigma\) is a curve in the \((f,g)\)-plane called contour; generically, \(h\) is an immersion of \(\Sigma\) outside of the pleats; at the pleat points, the contour has cusps.


(The contour on the left is a – rotated and somewhat distorted – rendition of Chicago Millenium Park’s Bean sculpture, with the cusps made visible.)
Pseudo-points, life contour, indices
As the coordinates on the \(f,g\) plane are given, more special points emerge: namely those where either of the functions has a critical point. We will be referring to these special points as V- (vertical) or H- (horizontal) points.
These H- and V-points sit on the critical curve \(\Sigma\). Generically, the functions \(f,g\) are Morse, and the contour has non-vanishing curvature at them. (This follows from the fact that at a critical point of, say \(f\) the restriction of Hessian matrix of \(f\) to the hyperplane \(\{dg=0\}\), is nondegenerate.)
The V- and H-points partition the critical curve into segments which map to the segments of the contour curve where its slope is \(\neq 0,\infty\). We will refer to the segments where the slope is negative as Pareto points (for obvious reasons).
We augment the Pareto segments by attaching at their boundaries the rays (referred to as extension rays) pointing up (at V-points) or right (at H-points). We will call the V- or H-points where this attachment results in \(C^1\) curve, the pseudosmooth points; those points where the curve loses smoothness, the pseudocusps.
We will refer to the resulting union of Pareto segments and extension rays as the life contour for the filtration defined by the pair \(f,g\).
At the points of Pareto segments one can coorient the contour, declaring positive the side where both\(f\) and\(g\) can increase. This allows one to define the index of a point \(x\) on the smooth part of Pareto segment: choose a function of \(f,g\) vanishing on contour near the point, and increasing in the positive direction; this function has a (degenerate) critical point at \(x\); its index is the index of the point \(p\).
The index at extension rays is defined just as the index of the critical point of \(f\) or \(g\), where the ray was attached to a Pareto segment.
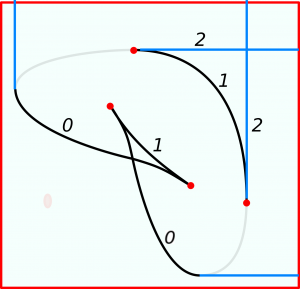
It is easy to see that the index is constant along the smooth parts of the Pareto segments, and jumps at cusps and pseudocusps in a predictable way: the higher with respect to \(f,g\) point has higher index.
Increasing curves and persistence
We will be referring to the (Pareto, i.e. such that the branches of the contour involved have negative slopes) pseudocusps, cusps and the double points of the same index) as obstacles.
Consider an increasing curve \(\gamma:\Real\to\Real^2\) in the \(f,g\)-plane (this means that both functions strictly increase along the curve). To fix the gauge, we will assume that the curve is parameterized by \(f+g\).
An increasing curve \(\gamma\) defines a usual \(I\)-indexed filtration of \(M\), and correspondingly, persistent homologies and persistent diagrams \(\phd_k(\gamma), k=0,\ldots,m\), which we interpret as a collections of distinguishable points in planes \(\{b\lt d\}\).
(Remark that the approach to multiparametric persistence through restriction to increasing straight lines has been considered by several authors. Here we allow arbitrary increasing curves.)
The main (somewhat tautological) result of this note is
Theorem: For the path-connected collection of increasing curves in the plane avoiding obstacles, there is a section of the space of persistent diagrams: that is for any two such curves \(\gamma,\gamma’\), there is an identification
\[
I(\gamma’,\gamma):\phd_*(\gamma)\to\phd_*(\gamma’),
\]
of the bars in the persistent diagrams corresponding to each of the curves, and these identifications are consistent:
\[
I(\gamma”,\gamma’)I(\gamma’,\gamma)=I(\gamma”,\gamma).
\]
Example
The figure below shows six homotopy non-equivalent increasing paths avoiding the obstacles, – five green and the sixth, blue.
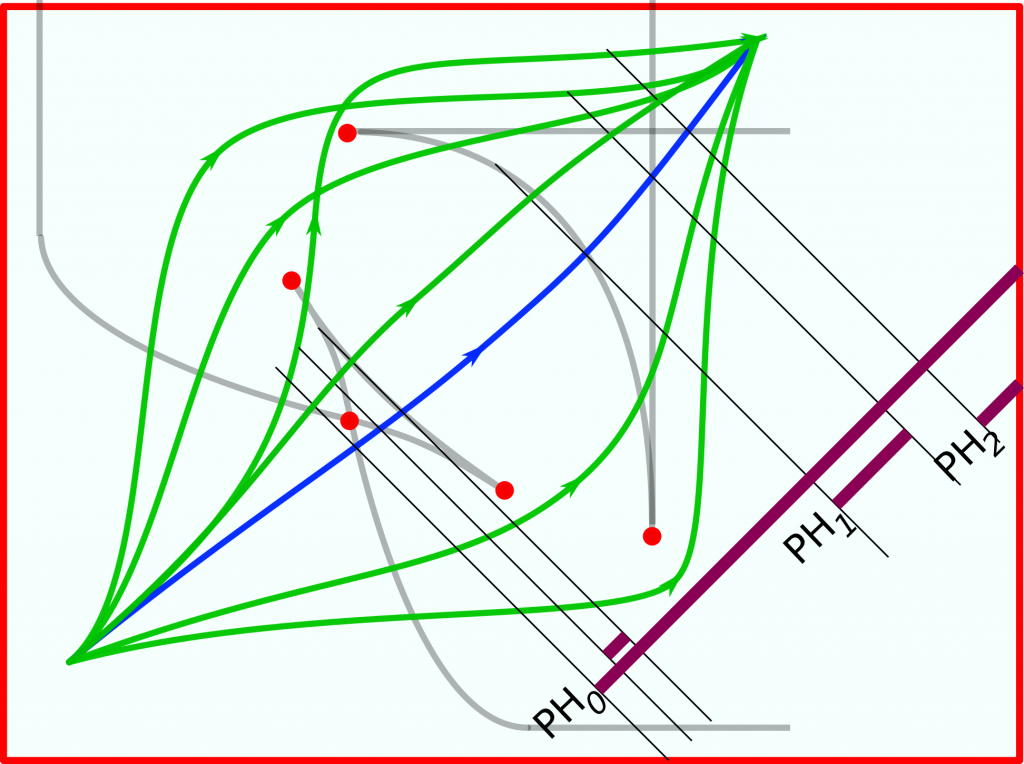
The bars shown on the lower left (recall that the curves are parameterized by \(f+g\) correspond to the filtration that the blue curve defines: the births and deaths happen where the curve intersects the life contour.
One can readily see what happens when one moves from one homotopy class to another, across a (pseudo)cusp with the indices of branches \((k,k+1)\): a bar in \(\phd_k\) appears or disappears.
As the curve crosses a self-intersection point of the life contour, where the branches of equal indices cross, one has a less prominent event, where the charges in the persistence diagram \(\phd_k\) bounce of a common vertical or horizontal line (we can call the corresponding bars interacting).
Increasing curves, obstacles and cubical complexes
This result prompts question about the structure of the space of increasing paths in the plane avoiding a finite collection of obstacles.
Theorem: the connected components of space of increasing curves in the plane avoiding a finite set of obstacles \(o_1,\ldots,o_k\in\Real^2\) are contractible, and their number is equal to the number of chains of obstacles, i.e. subsets \(o_{i_1}\prec\ldots o_{i_l}\), where \(o_m\prec o_n\) is the vector ordering of the points.
Adjacency of these cells is in itself an interesting invariant of the overall structure. Namely, for any collection of obstacles, consider the set of increasing paths passing through those obstacles. Each of these closed strata is manifestly contractible, as is (which is easy to prove the same way the Theorem above is proven) each connected component of the set of the increasing paths passing only through given set of obstacles.
Then the resulting stratification of the space of increasing paths is dual to a \(\CAT(0)\) cube complex: the vertices of the complex correspond to the connected components of teh set of increasing paths avoiding obstacles, and the sets \(h_k\) of increasing paths passing through obstacle \(o_k\) form the hyperplanes (for the nomenclature, see Sageev).
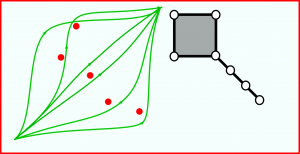
We will be referring to this cube complex as the characteristic complex of biparametric persistence structure defined by \(f,g\).
I would stipulate that the characteristic complex is the key descriptor of biparametric persistence in smooth category.
Problems
This note is but an introduction to the overall problem of understanding the nature of the characteristic complex for biparametric persistences. Here are a few research directions we hope to purse:
- How the characteristic complex changes under the small perturbations of the pair \(f,g\)? It is clear that cubes with all edges large survive (or cannot emerge out of nothing):
- Interacting bars: provide a combinatorial characterization in terms of the life contour.
- It is quite immediate that the characteristic complex survives smooth perturbations of \((f,g)\). As one deforms the pair, the structure of the characteristic complex changes in a predictable way (some vertices can appear/disappear; pairs of hyperplanes can appear/disappear etc). A study of these transformation would provide a good handle on the relation of the patterns of the characteristic complex.
- Relation of the characteristic complex and the invariants of biparametric persistence (as defined here or here) would be, obviously, of interest.
Postscriptum: A preprint is out.
